當氣體由一密封的小直徑管線尖端(或“探針”)向巖心切片表面,或非切片的整個巖樣,或可滲透的巖石露頭流動時,流動形態與半球狀流動有些相似(圖32)。這種流動狀態在小直徑影響范圍內,具有便宜、無損、零壓力的氣體滲透率測量而得到廣泛應用。如果巖心未清洗,也未干燥,測定的滲透率為未知油水飽和度的有效滲透率。這種測重是在密閉的空間中進行的,以確定非均質地層的
滲透率變化。進行這種測量的設備一般稱為“點式滲透率儀”或“迷你滲透率儀”。
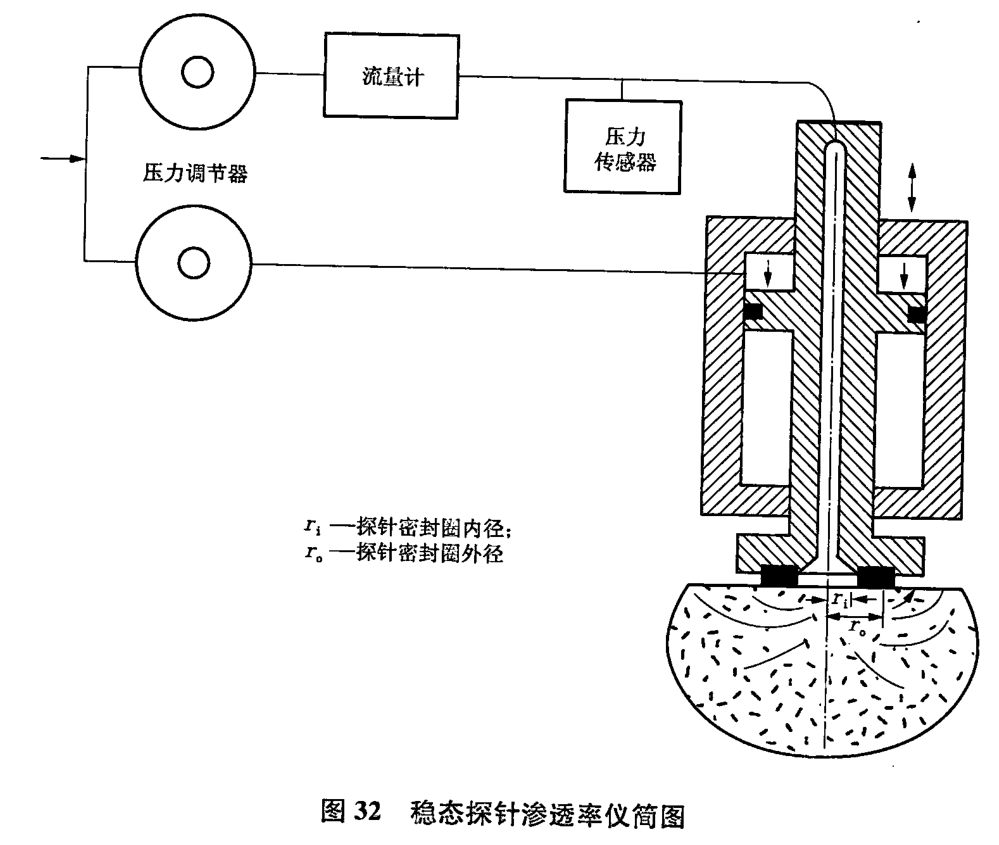
真正的半球狀流動幾何形態要求:)表面為較大平整均質的樣品;b)樣品在緊挨探針處應有半球狀內腔,其半徑,等于探針密封墊的內半徑;c)在探針與樣品接觸面以下樣品向各個方向延伸范圍很大(無限);)除半球的內腔外,平面的各處應是密封的。因為這些條件是不能完全實現的故Gogg等人[19進行了無因次幾何流動因子的數值計算,是在平整面較小、探針密封較小且內外半徑有限的小巖心上進行的。
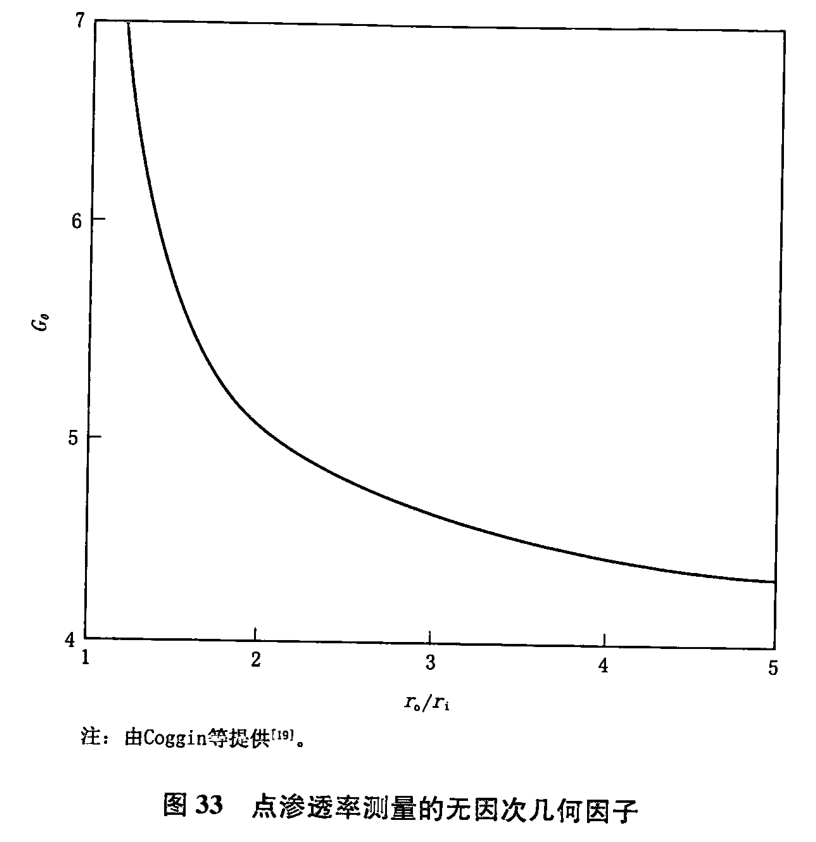
圖33表示無因次因子與探針密封墊的外半徑。與其內半徑的比值的關系。實際上,在較大巖樣上的半球流動時,G等于2π。圖33表示的關系可用于具有平整表面及對滲透率測定無影響的側向寬度和深度足夠大的外邊界樣品測試上。為實用目的,該因子只有在樣品的深度至少在4倍探頭內徑且從探頭軸心算起側向周邊至少在4倍內半徑的范圍時樣品測試才能產生較小的誤差,同時,如果探頭置于樣品的圓柱表面,并且具有嚴格的密封條件,那么樣品的半徑至少為12,同時樣品露頭部分的邊界有限時將產生更小的誤差。參見Goggin等人19關于與鄰近邊界有關的無因次幾何因子。

| 